Review written by Qiwei Yu (G2, Biophysics)
The stream of time flows inevitably forward and stops for no one. This one-way direction defines an “arrow of time”, which we perceive through the lens of irreversible processes that occur in both inanimate and living worlds. Irreversibility is manifested at both microscopic and macroscopic scales, ranging from the dissolution of an ink droplet in water to the concerted flight of large flocks of birds.
Irreversibility is especially important for biological systems, since many physiological functions require the directional flow of energy, material, or information. For example, many biological rhythms (such as circadian clocks) need to progress coherently and directionally forward. In some cases, irreversibility also gives us an idea of how much energy it takes to achieve certain biological functions. However, living systems are complex, making it a daunting task to quantify and understand the arrow of time either theoretically or experimentally.
In a recent article in Physical Review Letters [1,2], Dr. Christopher Lynn and colleagues from Princeton University and City University of New York pioneered an approach to greatly simplify this problem by decomposing the arrow of time, namely breaking down the total irreversibility of a complex system into contributions from discrete components and interactions among them. They demonstrated how this decomposition method overcomes the complexity of biological systems by applying it to previous experiments on the salamander retina, which led to intriguing findings.
Physicists quantify the arrow of time by the entropy production rate (EPR), which is a nonnegative quantity that describes irreversibility. The larger the EPR, the more irreversible a process. Its value can reach zero only when a process is fully reversible; for example, if a person is shown a movie of a process, he or she would not be able to tell whether the movie is played forward or backward. On the contrary, the larger the EPR, the easier it is for a person to discern forward trajectories from their backward counterparts. Therefore, the EPR is deeply connected to our own perception of irreversibility. To compute EPR, however, one essentially calculates probabilities of observing any forward and backward trajectories, which would require a large amount of data or measurements of the process, since the number of possible trajectories grows rapidly with the complexity of the system. Obtaining such large amounts of data is usually experimentally implausible for complex systems.
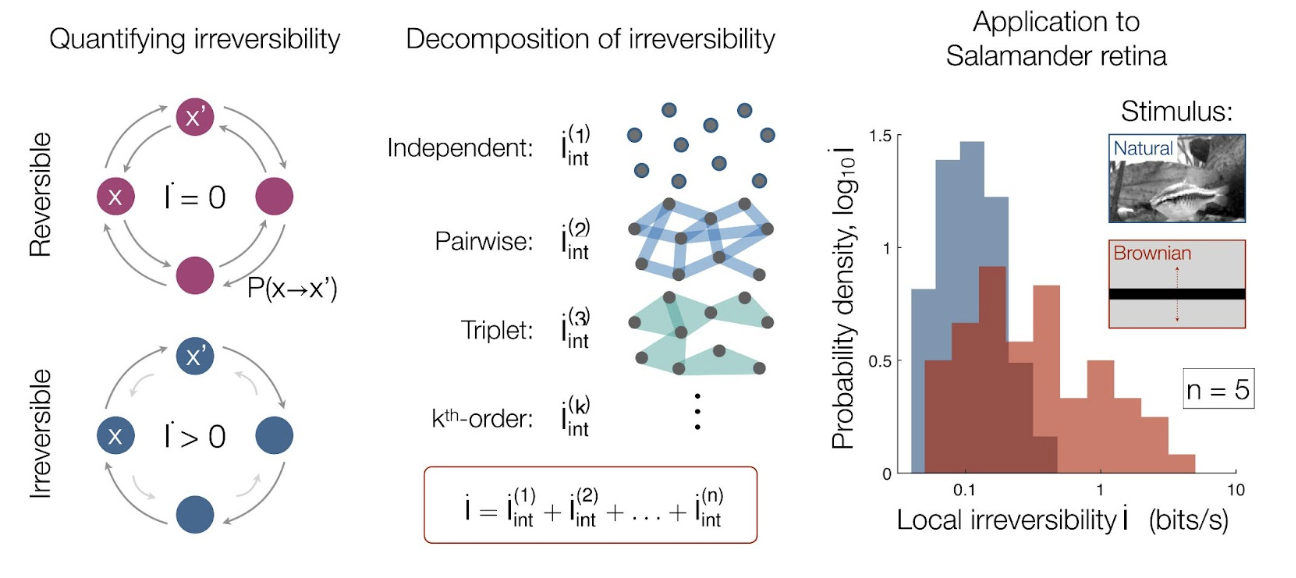
Lynn and colleagues showed that one can simplify the problem by breaking down irreversibility into smaller parts, each of which can be calculated with experimentally available statistics. This decomposition enables one to estimate the total irreversibility of a system, even with limited data. They showed that in a complex system with multiple components, the total irreversibility is the sum of contributions from the dynamics of each individual component and the interaction between multiple components. The latter can be further decomposed into contributions from the interaction between two components, three components, and so on. The irreversibility from individuals and few-component interactions only requires limited data to compute, making the method relevant to real experiments. Their sum provides a lower bound (minimum value) of the total irreversibility. As more and more interactions are considered, the lower bound approaches and thereby provides a better and better estimate of the total irreversibility.
Lynn et al. first illustrate the decomposition method in simple logical operations. What is more interesting, however, is the application to neurons in the salamander retina. These neurons not only react to visual stimuli from the outside world but also affect the activity of one another through directional synaptic couplings. Analyzing how irreversibility arises in these neurons is important for understanding visual information processing and, by extension, how we perceive irreversibility from what we see. To this end, the authors analyzed recordings of neuronal activity when the retina views different movies. These neuronal recordings are short in length, which prevents an accurate computation of the total irreversibility. In fact, the recording length needed to calculate the total irreversibility increases drastically with the number of neurons and quickly becomes experimentally inaccessible. With the decomposition, however, the authors were able to accurately compute the irreversibility for interactions involving up to five neurons with the available data.
In the salamander retina, Lynn et al. found that more than two-thirds of the total captured irreversibility comes from the pairwise interactions between every two neurons, and that this value diminishes as the interaction incorporates more neurons. This led the authors to conclude that the irreversibility due to higher-order interactions can be safely ignored since they only account for a small fraction of the total irreversibility. Thus, even in complex multi-neuronal systems, this work suggests that it is sufficient to consider few-neuron interactions for estimating the total irreversibility.
The most puzzling discovery arose when Lynn et al. compared the neuronal activity when the retina views movies with different inherent irreversibility (namely, movies of natural scenes, which are irreversible, and carefully designed movies of Brownian motion, which is a reversible process). Surprisingly, the comparison showed that more irreversibility is generated in the neurons themselves when they view the reversible Brownian movies. This indicates that the amount of irreversibility generated in the retina might be anti-correlated with the amount of irreversibility in the scene being viewed. The authors speculate that the retina might be adapted to processing natural scenes, which have high irreversibility. Therefore, it would cost the neurons more effort to process reversible movies, as they would be “surprising” to the system. Overall, the calculation of irreversibility provides a new perspective for understanding neural systems, especially how the retina functions.
Dr. Lynn’s work has been a significant step forward in physicists’ efforts toward understanding the arrow of time in living systems, which is necessary for them to maintain their structure and function. The complexity of this problem, however, comes in many flavors: biological systems involve not only interaction between multiple components, but also time and length scales spanning many orders of magnitude. Complementary to Dr. Lynn’s work, which focused on systems with many components, a previous study [3] also showed how dissipation varies with time and length scales in spatially and temporally extended biological systems such as biological clocks and active materials. Taken together, these advances are enabling researchers to better understand the irreversibility of complex living systems and, more importantly, how it helps achieve important biological functions.
“Princeton was integral to making this project a reality,” Dr. Lynn remarks when asked about the key factors contributing to the project’s success. “The Center for the Physics of Biological Function has supported this work at every step, not only financially but also by providing a rich environment for interactions between physicists and biologists and between theorists and experimentalists.” He is now expanding this interdisciplinary work in multiple directions. “From a neuroscience perspective, we have observed that the irreversibility of the retina does not simply increase with the irreversibility of the stimulus. But then what does neural irreversibility depend on? On the theoretical side, we're still very much interested in understanding how irreversibility and the arrow of time emerges in complex systems. For example, how does the entropy production scale as we coarse-grain a system? Questions such as these remain fundamentally unanswered.”
[1] C. W. Lynn, C. M. Holmes, W. Bialek, and D. J. Schwab, Physical Review Letters 129, 118101 (2022)
[2] C. W. Lynn, C. M. Holmes, W. Bialek, and D. J. Schwab, Physical Review E 106, 034102 (2022)
[3] Q. Yu, D. Zhang, and Y. Tu, Physical Review Letters 126, 080601 (2021)
Figure adapted from original articles, courtesy of Dr. Lynn.
The original article discussed here was published in Physical Review Letters on Sept 6, 2022, with a companion paper in Physical Review E published on the same day. Please follow this link and this link for the full articles.