Review written by Jaydeep Singh (MATH, G2)
Princeton scientists have long been at the forefront of research into nuclear fusion, a challenging process in which light atomic nuclei—hydrogen, for example—are chemically fused together to form heavier elements. The process releases immense amounts of energy, and is a promising approach for meeting the world’s energy needs. Early research dating from the post-war period explored designs for fusion-based weapons, but quickly interest turned to the process of harnessing fusion to generate usable electricity. Fusion research is a vast field encompassing both theoretical and experimental work, and it is not hard to see why controlled fusion remains a difficult problem after almost a century of progress: a prerequisite to achieving the fusion of light ions is the ability to super-heat the ions, in the form of a plasma, up to temperatures of 108 Kelvin within large reactors. To do this, all while maintaining the ability to confine and control the plasma, is no easy engineering feat.
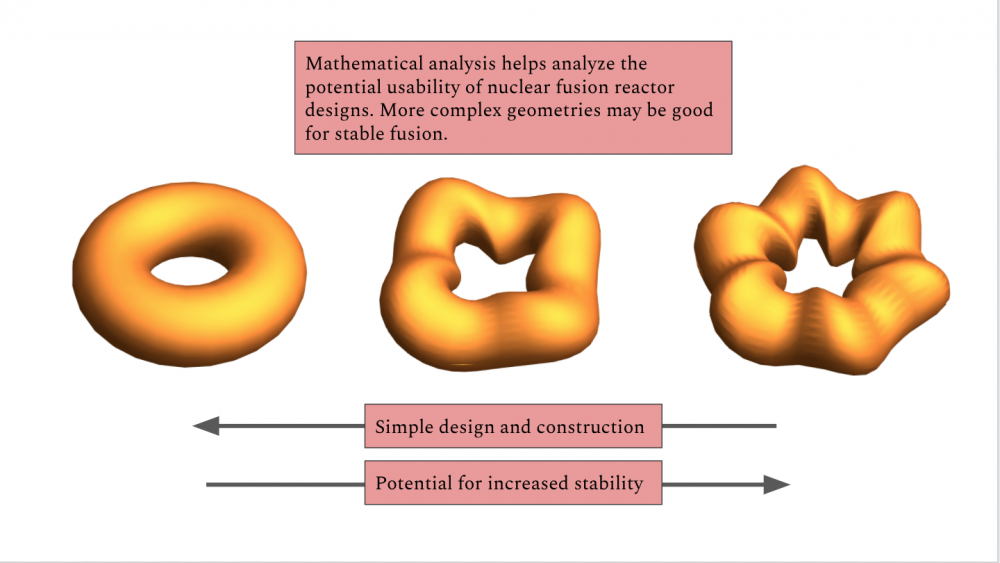
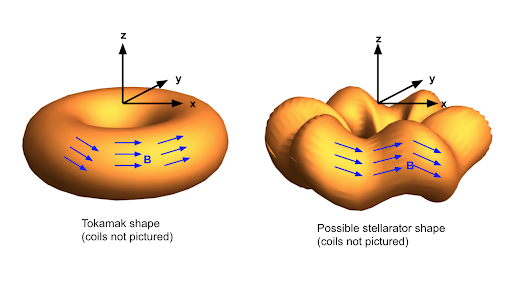
At the center of this challenge is a problem of geometry. The first step in realizing nuclear fusion is designing an appropriate reactor for housing the plasma. Reactor designs such as the tokamak (Fig. 1) employ donut-shaped (also known as toroidal) designs and complex arrays of magnetic coils to generate an external magnetic field capable of confining the plasma. It is this magnetic field, which we will denote B, that does the hard work of both ensuring the plasma stays away from the reactor walls and facilitating the particle collisions that spark the nuclear reaction. Tokamaks have been the dominant paradigm for several decades, cashing in on the simplicity of the shape to allow for scientists to optimize the shape in pursuit of confinement; however, this simplicity creates new engineering challenges as one tries to stabilize the plasma, and current models require additional large, electric currents that reduce the energy efficiency.
An alternative model is the stellarator (Fig. 1), which trades the symmetry of the tokamak—termed axi-symmetry—for a twisted exterior. The twists reduce many of the tokamak’s inefficiencies, but raise the question of whether appropriate magnetic fields might be constructed within the geometry to stably confine plasma. These stable configurations are called equilibria, and the viability of the stellarator rests on optimization techniques capable of identifying these magnetic equilibria. The search is therefore on for alternative geometries that utilize novel geometric features in order to overcome the tokamak’s key energy efficiency issues, while remaining simple enough to realistically study and build.
New work by mathematicians Peter Constantin and Daniel Ginsberg of Princeton’s Mathematics department, along with Theodore Drivas of Stony Brook University, revisits the question of how flexible stellarator geometries can be. Their analytical perspective allows for the application of tools from differential geometry and differential equations—subfields of pure mathematics research—to provide evidence that the solution space of magnetic equilibria may be incredibly rich. This result reveals that the physics of nuclear fusion has a deep mathematical structure, one that can be leveraged to find a zoo of new, viable stellarator designs.
The physics of plasma motion
The complexity of the space of equilibria is difficult to appreciate, because the physical equations governing magnetically charged plasmas are a system of nonlinear partial differential equations (PDE). PDEs are a mathematical language for studying dynamics of evolving physical systems, and their study comprises a main branch of mathematics and physics. The nonlinearity means that the terms of the equation interact with each other and with themselves, often leading to unpredictable behavior.
Stating our problem in the language of physics and PDEs, we model the behavior of our plasma as a gaseous fluid moved by large magnetic fields. The equilibria we are after are self-supporting magnetic fields that exist within the volume of the plasma. To find these, the authors apply a well known set of PDEs for plasma motion, called the Magnetohydrostatic (MHS) equations. Solving these (and herein lies the difficulty!) gives the magnetic field, a vector at each point that points in the direction of the plasma motion, that corresponds to the underlying geometry of the reactor T. Seen in this way, the (MHS) equations are a machine for going from the reactor T to the necessary magnetic field B.
Besides their nonlinear nature, much of the difficulty in solving these equations lies in these geometric conditions relating the analytic quantity, B, with the reactor geometry T. The authors are after equilibrium solutions that characterize confined plasmas, which imposes additional constraints on the possible solutions for B. One imagines the individual plasma ions as moving in the direction of the magnetic field B, so to ensure that the ions remain in the interior (as opposed to running into the walls) the authors impose that B should remain tangent, rather than perpendicular, to the boundary. Moreover, the magnetic field lines should “close up” on themselves as they move around the reactor.
The list of conditions goes on, and any hope of optimizing the stellarator’s geometry to allow for confining magnetic field solutions rests on a delicate balance of physics, geometry, and mathematical analysis. The authors’ analysis, however, proceeds by attacking a simpler problem. They do not take fully general stellerators and ask for solutions to the above MHS equations. Instead, they take inspiration from the plasma physics literature to look for a simpler subclass of solutions, called quasi-symmetric equilibrium solutions.
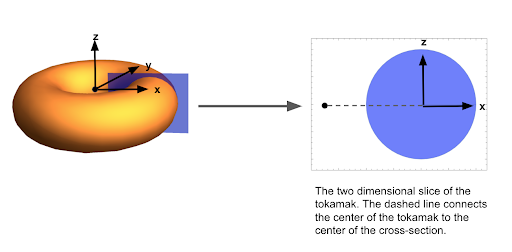
To better understand these, recall that the tokamak is a highly symmetric reactor design. In particular, it has a direction (the angular direction) along which the geometry is the same, and so one can search for solutions of the above MHS equations that respect this symmetry. In practice, this means that instead of solving the full three-dimensional problem for the magnetic field as a function of x,y,z coordinates, one uses symmetry to suppress one direction and solve the dimensionally reduced problem (see figure 2). It is exactly this insight that led the authors to consider stellarators with a special symmetry direction, along which one asks the magnetic field to be constant. While performing such symmetric reductions for wildly twisted stellarators is in practice quite complicated, this idea of searching a complicated space of solutions for ones with special properties (say, symmetry) is a common simplifying tool in both mathematics and physics.
Finally, we can state the problem as follows: given a stellarator geometry T’ that is symmetric along one direction, is there a quasi-symmetric equilibrium magnetic field B’ that solves the above MHS equations? Moreover, is it a physically reasonable solution that would effectively confine plasma?
Bringing in the mathematical machinery
The main result of the paper is phrased as a mathematical theorem, and roughly states that under certain mathematical assumptions, we can indeed solve the MHS equations in general geometries and find a magnetic equilibrium. More precisely, the authors show that starting from the tokamak, which is known to confine plasma, one can deform the geometry (imagine squashing or twisting the donut shape) and still find a magnetic equilibrium in the new reactor shape.
On a physical level, the result implies that given stellarator geometries that are themselves symmetric, and mostly in shape to the tokamak, there is hope of finding magnetic fields capable of confining plasma. A technical point is that the magnetic field constructed by the authors is only an approximate solution to the MHS equations, rather than an exact one. This implies that if these solutions were to be engineered, a small external force must be applied to maintain the plasma. The authors compute how large this force is, and are able to find situations in which it is small. However, this means that the original goal of locating exact equilibrium solutions remains open.
To appreciate the mathematical content of the result, it helps to look closer at the authors’ assumptions. The statement does not exactly address the problem described in the previous section, as the authors are not starting from an arbitrary symmetric reactor design. As is a common trick in the study of partial differential equations, the authors use as their starting point both the tokamak geometry T and a given solution B to the equations in that setting. Then, they prove that given this solution, under a suitably small geometric deformation (T to T’), they are able to construct a new solution B’ that works for the geometry T’. Formalizing this statement takes up much of the paper, and relies on coming up with the rigorous notion of what it means for two reactor geometries T and T’, or two magnetic fields B and B’, to be “close.”
Having stated the theorem, the authors turn to tools from a range of mathematical disciplines to locate a proof. One tool is a framework introduced by the same authors in a previous paper from 2020 [1]. This paper studies the problem of “flexibility” in solutions to the differential equations governing fluids (like plasmas). To see what this problem is, recall that equations like MHS are highly nonlinear, as the fluid interacts with both itself and the geometry of the reactor. It may therefore be a surprise that equilibrium solutions exist at all for certain geometries. Given such an exceptional solution (e.g. a confining magnetic field in the tokamak), what principle of the physics and the equation ensures that in a slightly deformed geometry there still exists a close-by equilibrium solution to the new problem? Mathematical results that show the existence of these close-by solutions reflect a natural flexibility in the equation.
The theorem therefore boils down to two parts: (1) identifying the exact partial differential equation that one must solve to locate quasi-symmetric equilibria in geometrically close domains T, T’, and (2) proving that this class of equations is “flexible” in the above sense. Part (2) is completed in paper [1], where it is shown that a wide class of PDEs (a subset of the very well-studied elliptic PDEs) are flexible under small deformations of the geometry. The insight of this new paper is that under the assumption of quasi-symmetry, the MHS equations reduce to another set that precisely satisfies the conditions of [1]. Combining the results, the authors conclude the theorem.
Next steps
By drawing on insights from their abstract study of the equations of fluid mechanics, the authors come tantalizingly close to one goal of fusion research: rigorous proof of quasi-symmetric (i.e. geometrically simple) equilibria that correspond to plasma confinement. Quasi-symmetric equilibria offer a possible way out of the tokamak’s energy efficiency problems, while hopefully remaining simple enough that engineers could produce the designs in the near future.The use of approximations at key steps of the authors’ argument prevents them from proving the full statement, but they suggest that modifications of their techniques may lead to a proof of full quasi-symmetry.
Addressing the implications of the work, Professor Drivas explains that, “In principle, our theorem provides a constructive method by which near-equilibria plasma configurations with good confinement properties may be built.” However, he cautions that actually building stellarators capable of producing these configurations remains a difficult mathematical and engineering challenge.
Although only one step in the larger story of nuclear fusion, the papers [1, 2] develop a wealth of ideas that may prove useful in ongoing research, both theoretical and experimental. Most importantly they contribute to the growing confidence in the potential of stellerators and other exotic geometries for achieving controlled fusion. No doubt mathematicians, applied and pure, will continue to be key contributors in the search for these new geometries.
This original article was published in the Journal of Plasma Physics on February 11, 2021. Please follow this link to view the full version.
References
[1] Constantin, P., Drivas, T.D., and Ginsberg, D. Flexibility and rigidity in steady fluid motion. Communications in Mathematical Physics (2021).
[2] Constantin, P., Drivas, T.D., and Ginsberg, D. On quasisymmetric plasma equilibria sustained by small force. Journal of Plasma Physics 87.1 (2021).